Cohen’s D is the difference between 2 means
expressed in standard deviations.
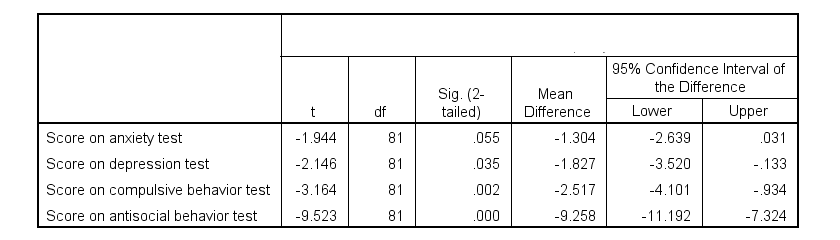
Children from married and divorced parents completed some psychological tests: anxiety, depression and others. For comparing these 2 groups of children, their mean scores were compared using independent samples t-tests. The results are shown below.

Some basic conclusions are that
However, what we really want to know is are these small, medium or large differences? This is hard to answer for 2 reasons:
A solution to both problems is using the standard deviation as a unit of measurement like we do when computing z-scores. And a mean difference expressed in standard deviations -Cohen’s D- is an interpretable effect size measure for t-tests.
Cohen’s D is computed as
$$D = \frac$$
where
But precisely what is the “pooled estimated population standard deviation”? Well, the independent-samples t-test assumes that the 2 groups we compare have the same population standard deviation. And we estimate it by “pooling” our 2 sample standard deviations with
Fortunately, we rarely need this formula: SPSS, JASP and Excel readily compute a t-test with Cohen’s D for us.
Running the exact same t-tests in JASP and requesting “effect size” with confidence intervals results in the output shown below.
Note that Cohen’s D ranges from -0.43 through -2.13. Some minimal guidelines are that
And there we have it. Roughly speaking, the effects for
We'll go into the interpretation of Cohen’s D into much more detail later on. Let's first see how Cohen’s D relates to power and the point-biserial correlation, a different effect size measure for a t-test.
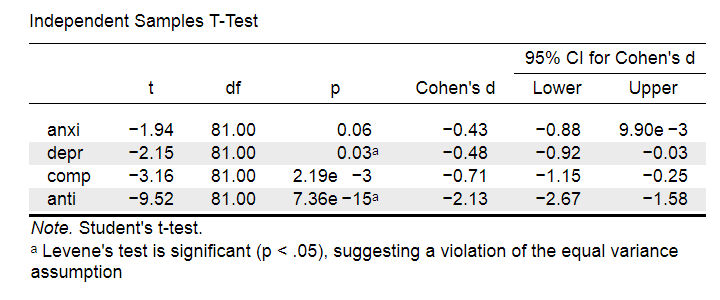
Very interestingly, the power for a t-test can be computed directly from Cohen’s D. This requires specifying both sample sizes and α , usually 0.05. The illustration below -created with G*Power- shows how power increases with total sample size. It assumes that both samples are equally large.
If we test at α = 0.05 and we want power (1 - β ) = 0.8 then
The assumptions for an independent-samples t-test are
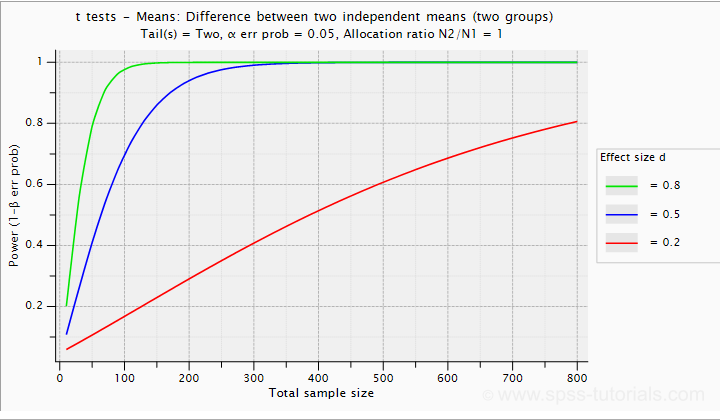
If assumptions 2 and 3 are perfectly met, then Cohen’s D implies which percentage of the frequency distributions overlap. The example below shows how some male population overlaps with some 69% of some female population when Cohen’s D = 0.8, a large effect.
The percentage of overlap increases as Cohen’s D decreases. In this case, the distribution midpoints move towards each other. Some basic benchmarks are included in the interpretation table which we'll present in a minute.
An alternative effect size measure for the independent-samples t-test is \(R_\), the point-biserial correlation. This is simply a Pearson correlation between a quantitative and a dichotomous variable. It can be computed from Cohen’s D with
$$R_ = \frac>$$
For our 3 benchmark values,
Alternatively, compute \(R_\) from the t-value and its degrees of freedom with
$$R_ = \sqrt>$$
The table below summarizes the rules of thumb regarding Cohen’s D that we discussed in the previous paragraphs.
| Cohen’s D | Interpretation | Rpb | % overlap | Recommended N |
|---|---|---|---|---|
| d = 0.2 | Small effect | ± 0.100 | ± 92% | 788 |
| d = 0.5 | Medium effect | ± 0.243 | ± 80% | 128 |
| d = 0.8 | Large effect | ± 0.371 | ± 69% | 52 |
Cohen’s D is available in SPSS versions 27 and higher. It's obtained from Analyze Compare Means Independent Samples T Test as shown below.
For more details on the output, please consult SPSS Independent Samples T-Test.
If you're using SPSS version 26 or lower, you can use Cohens-d.xlsx. This Excel sheet recomputes all output for one or many t-tests including Cohen’s D and its confidence interval from
The input for our example data in divorced.sav and a tiny section of the resulting output is shown below.
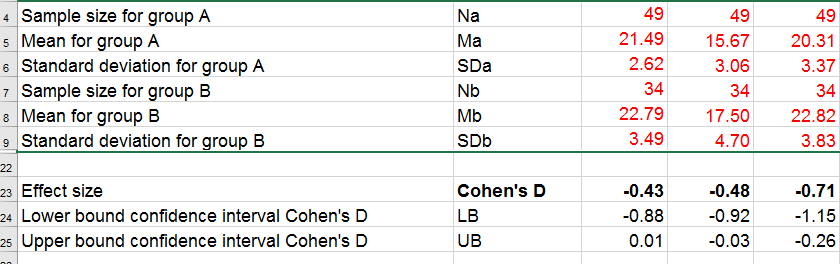
Note that the Excel tool doesn't require the raw data: a handful of descriptive statistics -possibly from a printed article- is sufficient.
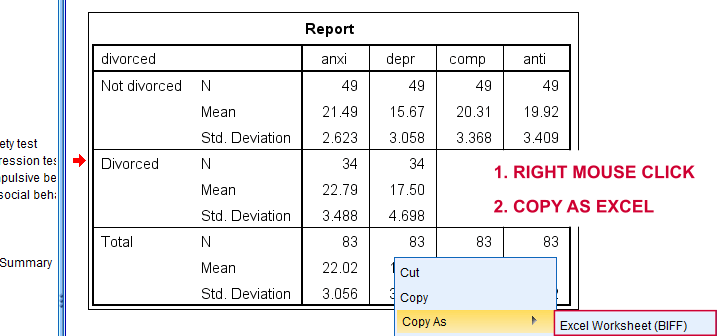
SPSS users can easily create the required input from a simple MEANS command if it includes at least 2 variables. An example is
*Create table with N, mean and SD for test scores by divorced for copying into Excel.
means anxi to anti by divorced
/cells count mean stddev.
Copy-pasting the SPSS output table as Excel preserves the (hidden) decimals of the results. These can be made visible in Excel and reduce rounding inaccuracies.
I think Cohen’s D is useful but I still prefer R 2 , the squared (Pearson) correlation between the independent and dependent variable. Note that this is perfectly valid for dichotomous variables and also serves as the fundament for dummy variable regression.
The reason I prefer R 2 is that it's in line with other effect size measures: the independent-samples t-test is a special case of ANOVA. And if we run a t-test as an ANOVA, η 2 (eta squared) = R 2 or the proportion of variance accounted for by the independent variable. This raises the question: why should we use a different effect size measure
if we compare 2 instead of 3+ subpopulations? I think we shouldn't.
This line of reasoning also argues against reporting 1-tailed significance for t-tests: if we run a t-test as an ANOVA, the p-value is always the 2-tailed significance for the corresponding t-test. So why should you report a different measure for comparing 2 instead of 3+ means?
But anyway, that'll do for today. If you've any feedback -positive or negative- please drop us a comment below. And last but not least:
thanks for reading!
WP JS USES THIS ID -->